[機械学習] AmazonのItem-to-ItemレコメンドをPythonで実装する
こんにちは、@yoheiMuneです。
本日はAmazonのレコメンドに関する論文で紹介されていたItem-to-Item Colaborative Filteringについて、こちらのブログ(英語)で実装イメージが載っていたので、Pythonで実装してみました。

ここでは
これを行列では以下のように表現することとします。
なおこのブログでは、行列表現にNumPyライブラリを使います。NumPyについては、[Python] 行列やベクトルを扱うことができるNumPyに入門でブログを書いていますので、そちらもご参照いただけましたら幸いです。
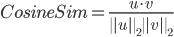
ここでは、SciPyライブラリに、コサイン距離(Cosine Distance)を求める機能があるので、それを利用します。
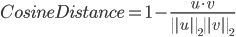
このデータをもとに、推薦結果を作成します。なお、アイテム6は顧客H以外は購入していないので、全く類似度はありません(このようなデータは今回の方法では推薦アイテムを生成できません)。
Amazon-Recommendations.pdf
How to Use Item-Based Collaborative Filters in Predictive Analysis
最後になりますが本ブログでは、フロントエンド・Python・機械学習など雑多に情報発信をしていきます。自分の第2の脳にすべく、情報をブログに貯めています。気になった方は、本ブログのRSSやTwitterをフォローして頂けると幸いです ^ ^。
最後までご覧頂きましてありがとうございました!
本日はAmazonのレコメンドに関する論文で紹介されていたItem-to-Item Colaborative Filteringについて、こちらのブログ(英語)で実装イメージが載っていたので、Pythonで実装してみました。

目次
Item-to-Item強調フィルタリングとは
強調フィルタリングの一種で、ユーザーの商品に対する行動を元データとして、レコメンドするアイテムを決定する仕組みです。ユーザーの行動とは、レビュー評価や購入などがあります。今回は「購入した」というデータとして、以下のようなデータを使いたいと思います。| アイテム | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 顧 客 | |||||||
| A | x | x | x | ||||
| B | x | x | |||||
| C | x | x | |||||
| D | x | x | x | ||||
| E | x | x | |||||
| F | x | x | x | x | |||
| G | x | x | |||||
| H | x | ||||||
xが購入したアイテムを、空欄が未購入のアイテムを意味ます。これを行列では以下のように表現することとします。
>>> import numpy as np
>>> x = np.array([
[1,1,1,0,0,0],
[1,1,0,0,0,0],
[0,0,1,0,1,0],
[0,0,1,1,1,0],
[0,1,1,0,0,0],
[1,1,0,1,1,0],
[1,0,1,0,0,0],
[0,0,0,0,0,1]
])
このデータから、アイテム1〜アイテム6のそれぞれについて、レコメンドするべきアイテムを計算してみたいと思います。なおこのブログでは、行列表現にNumPyライブラリを使います。NumPyについては、[Python] 行列やベクトルを扱うことができるNumPyに入門でブログを書いていますので、そちらもご参照いただけましたら幸いです。
Item-to-Item強調フィルタリングを実装する
ここでは、アイテムに対するユーザー評価をまとめて、1つのベクトルとして扱います。例えばアイテム1とアイテム2のそれぞれ、ベクトルは以下の通りとなります。# アイテム1のベクトル表現 >>. x.T[0] array([1, 1, 0, 0, 0, 1, 1, 0]) # アイテム2のベクトル表現 >> x.T[1] array([1, 1, 0, 0, 1, 1, 0, 0])そして、この2つのベクトルの距離を計算して、ベクトルの近さを求めます。ここではコサイン類似度(Cosine Similarity)を用います。
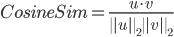
ここでは、SciPyライブラリに、コサイン距離(Cosine Distance)を求める機能があるので、それを利用します。
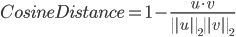
>>> from scipy.spatial.distance import cosine >>> item1 = x.T[0] >>> item2 = x.T[1] >>> sim = 1 - cosine(item1, item2) >>> print(sim) 0.75これでアイテム1とアイテム2の距離を計算することができました。この調子で、全てのアイテムについてそれぞれの距離を計算します。この計算については、Scipyの
pdist関数を用いることで一気に計算することができます。>>> from scipy.spatial.distance import pdist >>> # アイテムを行に、ユーザーを列に転置する >>> x = x.T >>> # 行ごと(=つまりアイテムごと)の距離を計算する >>> d = pdist(x, 'cosine') >>> # 「類似度 = 1 - 距離」 >>> d = 1 - d >>> print(d) [ 0.81649658 0.40824829 0.33333333 0.81649658 0.57735027 0.81649658 0. 0. 0. 0.5 0.70710678 0.5 0. 0.81649658 0.5 0.35355339 0.5 0. 0.40824829 0.57735027 0.40824829 0. 0.35355339 0.5 0. 0.35355339 0. 0. ]各アイテムの類似度が出ましたが、結果がベクトルで見づらいので、行列に変換します。
>>> from scipy.spatial.distance import squareform >>> d = squareform(d) >>> print(d) [[ 0. 0.75 0.4472136 0.35355339 0.28867513 0. ] [ 0.75 0. 0.4472136 0.35355339 0.28867513 0. ] [ 0.4472136 0.4472136 0. 0.31622777 0.51639778 0. ] [ 0.35355339 0.35355339 0.31622777 0. 0.81649658 0. ] [ 0.28867513 0.28867513 0.51639778 0.81649658 0. 0. ] [ 0. 0. 0. 0. 0. 0. ]]同一アイテム同士(アイテム1とアイテム1など)は計算されていないので一律0ですが、それ以外は類似度の計算ができました。これを見やすくテーブル形式にすると以下のデータ隣ます。
| アイテム | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| ア イ テ ム | |||||||
| 1 | 0. | 0.75 | 0.4472136 | 0.35355339 | 0.28867513 | 0. | |
| 2 | 0.75 | 0. | 0.4472136 | 0.35355339 | 0.28867513 | 0. | |
| 3 | 0.4472136 | 0.4472136 | 0. | 0.31622777 | 0.51639778 | 0. | |
| 4 | 0.35355339 | 0.35355339 | 0.31622777 | 0. | 0.81649658 | 0. | |
| 5 | 0.28867513 | 0.28867513 | 0.51639778 | 0.81649658 | 0. | 0. | |
| 6 | 0. | 0. | 0. | 0. | 0. | 0. | |
推薦結果を作成する
上記で計算したコサイン類似度をもとにアイテム1〜アイテム6までそれぞれの推薦結果を作成します。ここでは類似度の高い上位3アイテムを推薦対象にしています。
>>> # 自分自身は対象外にしたいので、優先度を下げる
>>> me = np.eye(d.shape[0])
>>> d = d - me
>>> print(d)
[[-1. 0.75 0.4472136 0.35355339 0.28867513 0. ]
[ 0.75 -1. 0.4472136 0.35355339 0.28867513 0. ]
[ 0.4472136 0.4472136 -1. 0.31622777 0.51639778 0. ]
[ 0.35355339 0.35355339 0.31622777 -1. 0.81649658 0. ]
[ 0.28867513 0.28867513 0.51639778 0.81649658 -1. 0. ]
[ 0. 0. 0. 0. 0. -1. ]]
# item1〜6まで、類似度の高い順に3つ推薦対象とする
>>> for idx in range(x.shape[0]):
print("item%d"%(idx+1))
item1_sim = d[:,idx]
# print(item1_sim)
item1_rel = []
for i in range(item1_sim.shape[0]):
item1_rel.append(('item%d'%(i+1), item1_sim[i]))
item1_rel = sorted(item1_rel, key=lambda d:d[1], reverse=True)
# 3件に絞る
item1_rel = item1_rel[:3]
print(" ", item1_rel)
print("")
# 出力結果例
item1
[('item2', 0.75), ('item3', 0.44721359549995787), ('item4', 0.35355339059327373)]
item2
[('item1', 0.75), ('item3', 0.44721359549995787), ('item4', 0.35355339059327373)]
item3
[('item5', 0.5163977794943222), ('item1', 0.44721359549995787), ('item2', 0.44721359549995787)]
このようにして、Item-to-ItemCFでは事前に商品ごとに推薦対象を作成することができます。素敵ですね。参考資料
今回の実装を行うために、以下の記事を参照しました。ありがとうございます。Amazon-Recommendations.pdf
How to Use Item-Based Collaborative Filters in Predictive Analysis
最後に
今回はAmazonのアイテムtoアイテムの強調フィルタリングレコメンドの実装をブログに書きました。実際にはNMFやSVDを組み合わせたり、他のレコメンドロジックを組み合わせたりと色々とするとのことですが、それらはこれからボチボチと取り組めたらと考えています。そのうちブログに書きたいと思います。最後になりますが本ブログでは、フロントエンド・Python・機械学習など雑多に情報発信をしていきます。自分の第2の脳にすべく、情報をブログに貯めています。気になった方は、本ブログのRSSやTwitterをフォローして頂けると幸いです ^ ^。
最後までご覧頂きましてありがとうございました!




